Στατιστική στην Εκπαιδευτική Έρευνα

2ο μάθημα

Αλέξανδρος Ρέκκας

2025-10-17

Ανακεφαλαιωτικά

Κλίμακες μέτρησης

• Ονομαστική
• Διατάξιμη
• Ισοδιαστημική
• Αναλογική

Συχνότητα

Μετρήσεις μεταβλητής \[X = [4, 5, 5, 6, 6, 6, 7, 8, 8, 9]\]

• Συχνότητα \(f(x_i)\): πόσες φορές εμφανίζεται η τιμή \(x_i\), π.χ. η τιμή \(x_1=4\)
• Σχετική συχνότητα \(f_r(x_i) = \frac{f(x_i)}{n}\)
• Ποσοστιαία συχνότητα: \(f_\%(x_i) = 100\times f_r(x_i)\)

Πίνακας συχνοτήτων

Τιμή	\(f\)	\(f_r\)	\(f_\%\)
4	1	0.10	10%
5	2	0.20	20%
6	3	0.30	30%
7	1	0.10	10%
8	2	0.20	20%
9	1	0.10	10%
Σύνολο	10	1.00	100%

Γραφική αναπαράσταση

Ιστογράμματα

• Για ποσοτικές μεταβλητές (ισοδιαστημικές/αναλογικές).
• Οριζόντιος άξονας: κλάσεις/διαστήματα τιμών.
• Κατακόρυφος άξονας: συχνότητες (ή σχετικές/ποσοστιαίες).
• Οι στήλες εφάπτονται (συνεχής κλίμακα).

Ιστογράμματα

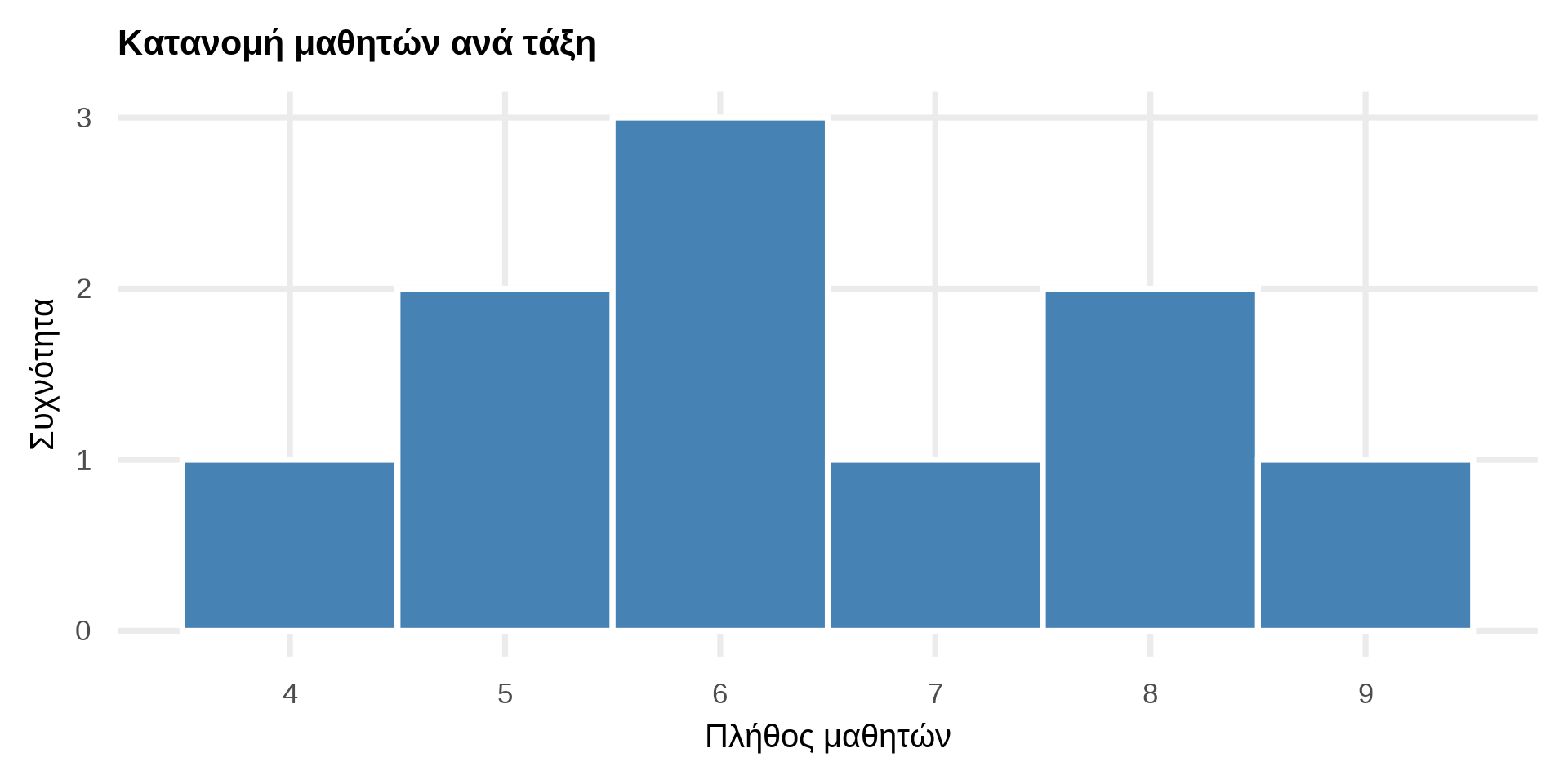
Ιστόγραμμα κατανομής μαθητών ανά τάξη

Πολύγωνο συχνοτήτων

• Σημειώνουμε το κέντρο κάθε κλάσης.
  
• Συνδέουμε τα σημεία κατά σειρά → πολύγωνο.
  
• Χρήσιμο για σύγκριση δύο κατανομών στο ίδιο γράφημα.

Πολύγωνο συχνοτήτων

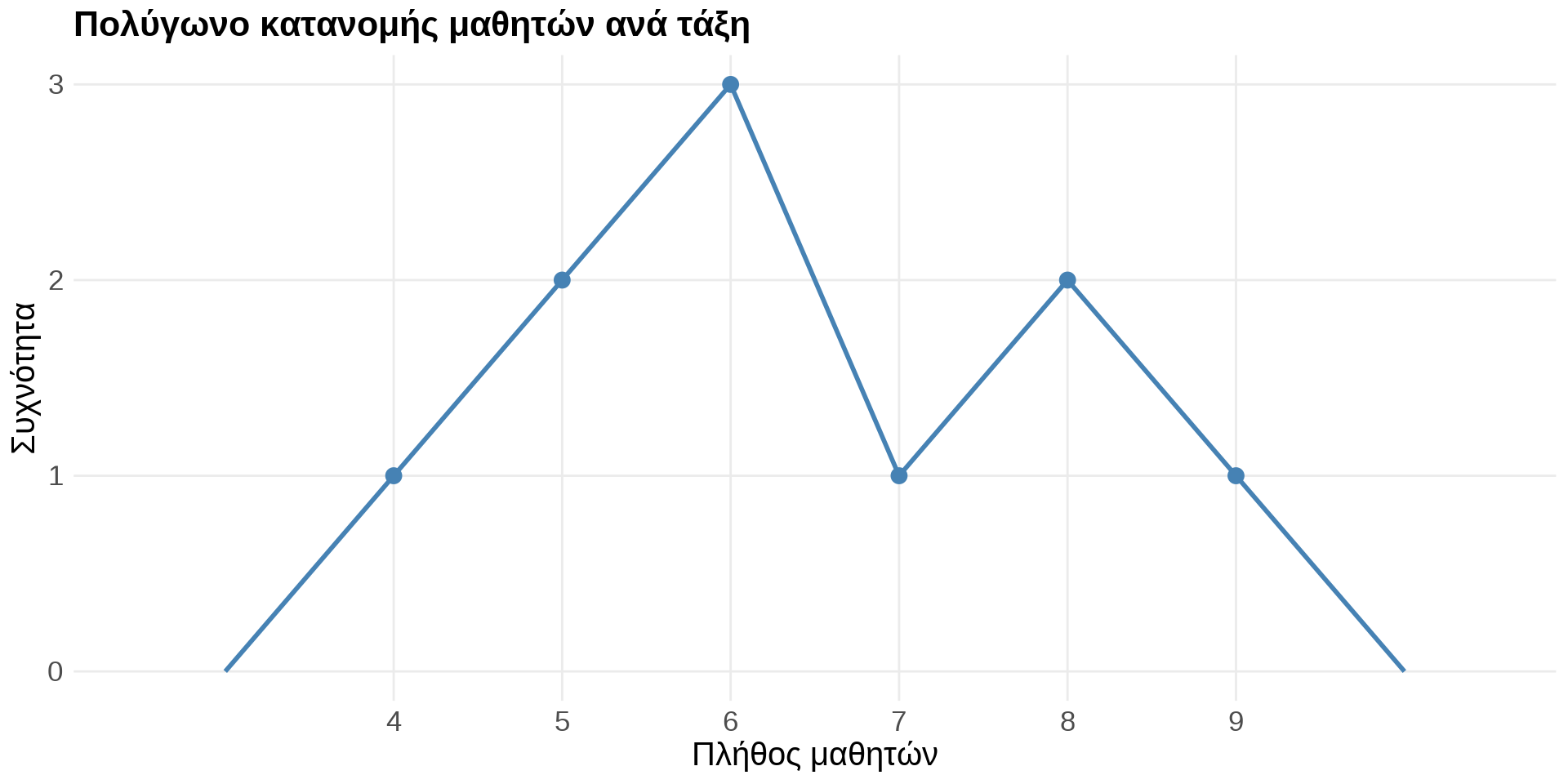
Ιστόγραμμα κατανομής μαθητών ανά τάξη

Παράδειγμα

Δεδομένα (ύψη σε cm):
95, 100, 102, 105, 108, 110, 112, 115, 118, 120, 121, 123, 125

Ραβδογράμματα

• Για ονομαστικές ή διατάξιμες μεταβλητές.
• Οι στήλες ΔΕΝ εφάπτονται.
• Η σειρά μπορεί να είναι αλφαβητική ή κατά συχνότητα.
  
• Οι άξονες: κατηγορίες (x), συχνότητα/ποσοστό (y).

Παράδειγμα

Έρευνα στην τάξη: «Αγαπημένο παιχνίδι»

Κατηγορία	Συχνότητα
Τουβλάκια	9
Κούκλες	7
Παζλ	4
Αυτοκινητάκια	6

Μέτρα θέσης

Γενικά

Στόχος

Να περιγράψουμε κεντρική τάση μιας κατανομής. Δηλαδή, να βρούμε εκείνη την τιμή γύρω από την οποία συγκεντρώνονται οι τιμές μιας μεταβλητής

Μέτρα θέσης:

• Μέση τιμή
• Διάμεσος
• Επικρατούσα τιμή

Μέση τιμή

Για τιμές \(x_1, x_2, \dots, x_n\):

\[ \bar{x}=\frac{1}{n}\sum_{i=1}^{n} x_i = \frac{x_1+x_2+\dots + x_n}{n} \]

• Χρησιμοποιείται για ισοδιαστημικές/αναλογικές μεταβλητές
• Ευαίσθητος στις ακραίες τιμές

Παράδειγμα

Δεδομένα: \(Χ = [10, 10, 10, 20, 20]\)

\[ \bar{x}=\frac{10+10+10+20+20}{5}=\frac{70}{5}=14 \]

Άσκηση

Έστω ότι έχουμε το ιστόγραμμα:

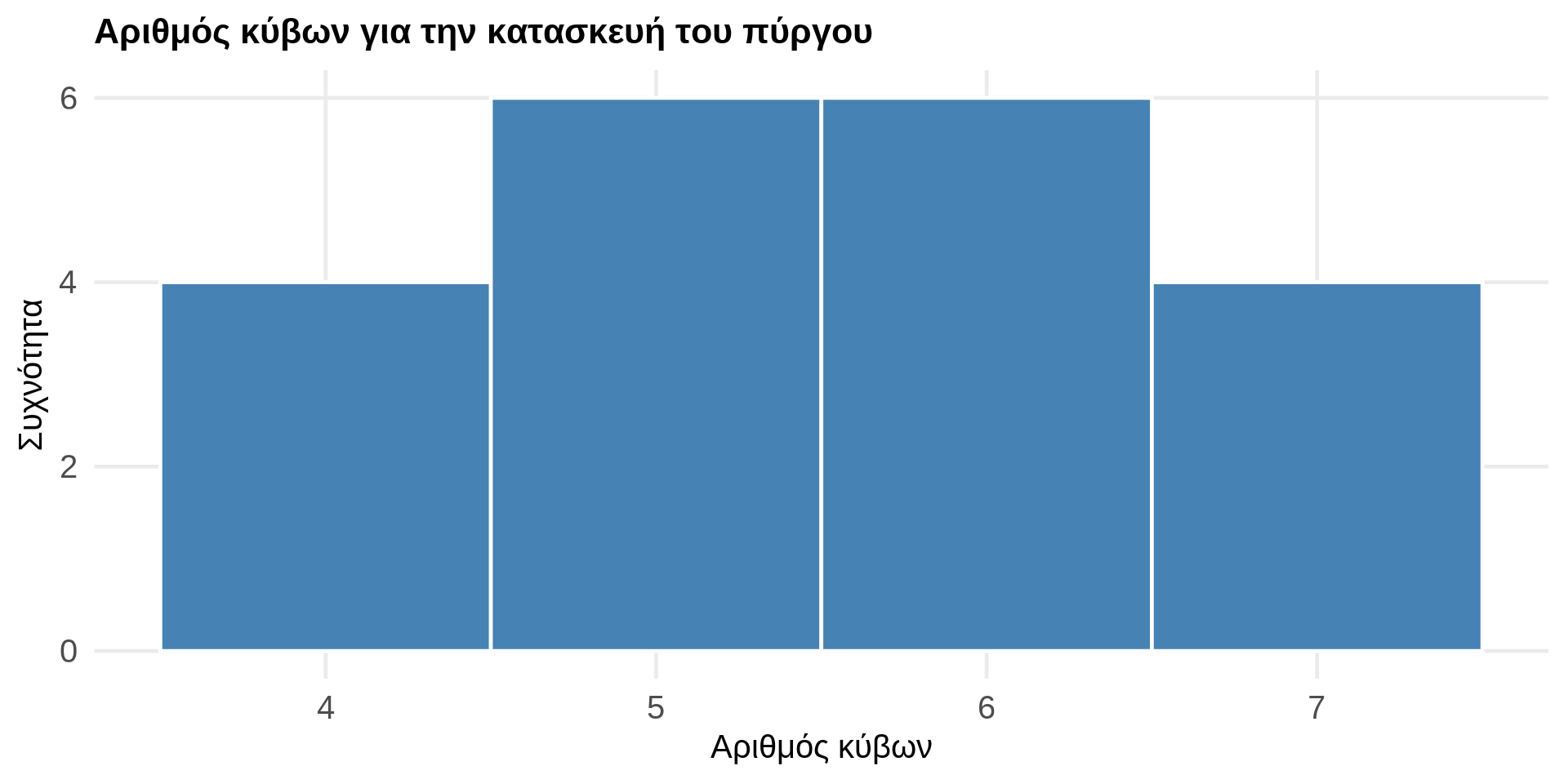
Υπολογίστε τη μέση τιμή του δείγματος.

Διάμεσος

Η μεσαία τιμή μιας μεταβλητής.

Υπολογισμός:

• Ταξινομούμε τις τιμές σε αύξουσα σειρά
• Αν \(n\) είναι περιττός αριθμός: η μεσαία τιμή
• Αν \(n\) είναι άρτιος (ζυγός) αριθμός: ο μέσος όρος των δύο μεσαίων

Παράδειγμα (περιττό \(n=5\)):

\[(3, 5, 7, 8, 12 \Rightarrow \tilde{x}=7)\]

Παράδειγμα (ζυγό \(n=6\)):

\[(2, 4, 5, 7, 9, 11 \Rightarrow \tilde{x}=(5+7)/2=6)\]

Παράδειγμα

Βρες τη διάμεσο: \(Χ = [4, 9, 1, 3, 7, 7, 2]\)

Ερώτηση

Τι θα γίνει αν προσθέσουμε τιμή 100;

Επικρατούσα τιμή

• Η τιμή που εμφανίζεται πιο συχνά
• Μπορεί να υπάρχει μία (μονοτροπική), δύο (διτροπική) ή καμία (όλες μοναδικές).
• Μπορεί να χρησιμοποιηθεί και για κατηγορικές μεταβλητές (ονομαστική ή διατάξιμη κλίμακα)

Παράδειγμα

Χώρος ελεύθερου παιχνιδιού	\(f\)	\(f_\%\)
Γωνιά με τουβλάκια	12	30.0
Δραματικό παιχνίδι (κουκλόσπιτο/στολές)	9	22.5
Καλλιτεχνικό εργαστήριο (ζωγραφική/χειροτ.)	7	17.5
Γωνιά ανάγνωσης	6	15.0
Τραπέζι πειραμάτων	4	10.0
Υπαίθριο παιχνίδι	2	5.0
Σύνολο	40	100.0

Παράδειγμα

Κατηγορία (Φρούτο κολατσιού)	Συχνότητα (n)	Ποσοστό (%)
Μήλο	10	25.0
Μπανάνα	10	25.0
Σταφύλι	8	20.0
Πορτοκάλι	6	15.0
Αχλάδι	6	15.0
Σύνολο	40	100.0

Σύνοψη

Τύπος δεδομένων	Κατάλληλο γράφημα
Ποσοτικές (ισοδιαστημικές/αναλογικές)	Ιστόγραμμα + Πολύγωνο
Κατηγορικές (ονομαστικές/διατάξιμες)	Ραβδόγραμμα

Σύνοψη

Κλίμακα μέτρησης	Κατάλληλο μέτρο θέσης
Ονομαστική	Επικρατούσα τιμή
Διατάξιμη	Διάμεσος και επικρατούσα τιμή
Ισοδιαστημική Αναλογική	Μέση τιμή (αν δεν υπάρχουν ακραίες), Διάμεσος (αν υπάρχουν)

Ευχαριστώ!